19 febbraio 2021. L'acqua non soltanto è la sostanza presente più in abbondanza sul pianeta Terra e negli organismi viventi, ma anche quella che ha caratteristiche veramente eccezionali: sono proprio queste caratteristiche che ne spiegano l'importanza per l'esistenza stessa della vita sul nostro pianeta. Merita di essere meglio conosciuta da tutti sin dall'età dell'infanzia. E' per questo motivo che stimolo i miei nipotini a continuarne l'esplorazione...
Continuiamo a utilizzare le monetine da 1 centesimo, ma non solo quelle. Chiediamoci: che cosa succede se versiamo l'acqua goccia a goccia sulle monetine? Ma, prima ancora, cominciamo ad osservare le gocce mentre le versiamo, una alla volta, sulle monete. Che forma hanno? Miriam ed Abi si mettono subito al lavoro, mentre Sara osserva a distanza, e con una certa aria di sufficienza...
Devono prendere una certa dimestichezza con l'uso accorto del contagocce: non devono aver fretta ed essere precisi e attenti nelle piccole operazioni materiali a loro assegnate. Cerco di responsabilizzarli, dicendo loro che stiamo lavorando come gli scienziati veri nei loro laboratori super-attrezzati: noi siamo – è vero – in un ambiente domestico e abbiamo materiali e strumenti di poco valore, ma dobbiamo seguire lo stesso metodo sperimentale che caratterizza l'indagine scientifica. I nipotini si galvanizzano ancora di più: pasticciano a volte, a volte sono troppo precipitosi, ma nel complesso si comportano bene.
Utilizzando i loro disegni e commentando le loro osservazioni, ci accordiamo nel dire che le gocce, all'inizio del distacco dal contagocce, hanno una forma quasi sferica. Man mano, però, si deformano sino a che, nel distaccarsi definitivamente, appaiono come “ristrette” in alto e un po' “spanciate” in basso. Questa deformazione è dovuta proprio alla loro caduta per effetto della gravità. In un ambiente isolato e indifferente alla gravità avrebbero una forma perfettamente sferica: la sfera non privilegia alcuna direzione e assicura a tutte le particelle di acqua che compongono una goccia lo “stesso trattamento”. La sfera è il solido più pieno: è il solido che racchiude il massimo volume in una determinata superficie.

GOCCIA
Versiamo, ora, con la massima attenzione le gocce sulla superficie delle monetine da 1, 2, 5, 10 e 50 centesimi. Quante gocce riusciremo a versare senza che l'acqua trabocchi? Miriam ed Abi operano individualmente sotto la sorveglianza mia e di Sara. Con il contagocce facciamo sì che l'acqua scorra lentamente dalla parte inferiore del tubicino. Gli scienziati che hanno studiato il fenomeno assicurano che la goccia cade quando supera una certa dimensione, e quindi un certo peso, che dipende dalla tensione superficiale del liquido e dal diametro del tubicino. Verifichiamo, dunque, come sia importante questa caratteristica dell'acqua chiamata “tensione superficiale”, che ci ha consentito di introdurre tante monetine in un bicchiere d'acqua (V. esperimento del 12 febbraio)...
MONETINE
Facendo una media delle diverse prove effettuate sulle monetine, possiamo riferire questi risultati. Sulle monetine da 1, 2, 5, 10 e 50 centesimi abbiamo versato – rispettivamente - 16, 20, 25, 28, 50 gocce. Avvertenza importante: i risultati cambiano sensibilmente non soltanto da sperimentatore a sperimentatore, ma anche a seconda del contagocce utilizzato e della “pulizia” delle monetine.
Chiediamoci, ora, qual è il volume di acqua che abbiamo depositato su queste monetine. Lo possiamo stabilire solo quando sapremo il volume di ogni singola goccia. E per saperlo ricorriamo ad una siringa, privata dell'ago, che riempiremo sino al segno di 2 ml. Risultato medio ottenuto: 40 gocce in 2 ml. Una goccia occupa il volume di 0,05 ml. Le gocce mediamente versate su ogni monetina occupano i seguenti volumi espressi in ml: 0,8; 1,0; 1,25; 1,4; 2,5.
Ora confrontiamo questi volumi di acqua con il volume di ogni monetina che ricaviamo dai dati forniti dalla Zecca di Stato (V. tabella). A questo punto interviene Sara, che frequenta la prima classe del liceo scientifico: ci viene in soccorso fornendo la formula per calcolare il volume di un cilindro di cui siano note le misure del diametro e dell'altezza: raggio x raggio x 3,14 x altezza; utilizza la calcolatrice e ci fornisce i risultati (V. tabella).
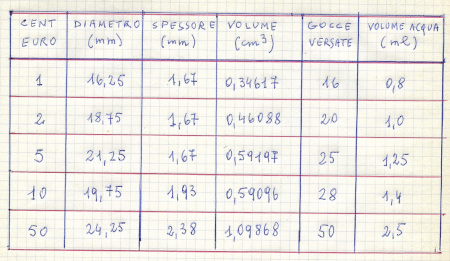
Tabella MONETINE
Posta l'equivalenza 1 cm al cubo = 1 ml, ci sorprendiamo di quanto più grande sia il volume dell'acqua versata rispetto al volume delle monetine sottostanti. Veramente sorprendente la forza di coesione che dimostrano di avere fra loro le particelle microscopiche - molecole, per i chimici – di questa straordinaria sostanza che è l'acqua! Forza di coesione che determina il valore elevato della sua tensione superficiale.
Per dimostrare, ulteriormente, che le particelle microscopiche di acqua si “sentono” fra loro e tendono a rimanere il più possibile unite, mostro ai miei nipotini delle foto scattate recentemente in questi ultimi giorni d'inverno. Le foto mi servono anche per preannunciare l'argomento del prossimo appuntamento: le gocce di pioggia.
PERLE d'ACQUA
Venerdì 19 Febbraio,2021 Ore: 18:01